Home
Trigonometric Functions
Radians are the arc length of a unit circle.
- $180^\circ = \pi * radians$
Trig functions are defined as the ratio of 2 sides of a right angle.
| Soh |
Cah |
Toa |
| $\sin{\theta} = \frac{opp}{hyp}$ |
$\cos{\theta} = \frac{adj}{hyp}$ |
$\tan{\theta} = \frac{opp}{adj}$ |
| $\csc{\theta} = \frac{hyp}{opp}$ |
$\sec{\theta} = \frac{hyp}{adj}$ |
$\cot{\theta} = \frac{adj}{opp}$ |
Trig Identities
Other Identities
| Even/Odd |
Even/Odd |
Reciprocal |
Quotient |
| $\sin{(-\theta)} = -\sin{\theta}$ |
$\csc{(-\theta)} = -\csc{\theta}$ |
$\csc{\theta} = \frac{1}{\sin{\theta}}$ |
$\tan{\theta} = \frac{\sin{\theta}}{\cos{\theta}}$ |
| $\cos{(-\theta)} = \cos{\theta}$ |
$\sec{(-\theta)} = \sec{\theta}$ |
$\sec{\theta} = \frac{1}{\cos{\theta}}$ |
$\cot{\theta} = \frac{\cos{\theta}}{\sin{\theta}}$ |
| $\tan{(-\theta)} = -\tan{\theta}$ |
$\cot{(-\theta)} = -\cot{\theta}$ |
$\cot{\theta} = \frac{1}{\tan{\theta}}$ |
|
Pythagorean Identities
- $\sin^{2}{\theta} + \cos^{2}{\theta} = 1$
- $1 + \tan^{2}{\theta} = \sec^{2}{\theta}$
- $1 + \cot^{2}{\theta} = \csc^{2}{\theta}$
Sum and Difference
- $\sin{(\theta_1 \pm \theta_2)} = \sin{\theta_1} \cos{\theta_2} \pm \cos{\theta_1} \sin{\theta_2}$
- $\cos{(\theta_1 \pm \theta_2)} = \cos{\theta_1} \cos{\theta_2} \mp \sin{\theta_1} \sin{\theta_2}$
- $\tan{(\theta_1 \pm \theta_2)} = (\tan{\theta_1} \pm \tan{\theta_2}) / (1 \mp \tan{\theta_1} \tan{\theta_2})$
$\mp$ means the opposite sign as the $\pm$ before it.
- Ex: $6\pm(2\mp4) = 6 + (2 - 4)$ or $6 - (2 + 4)$
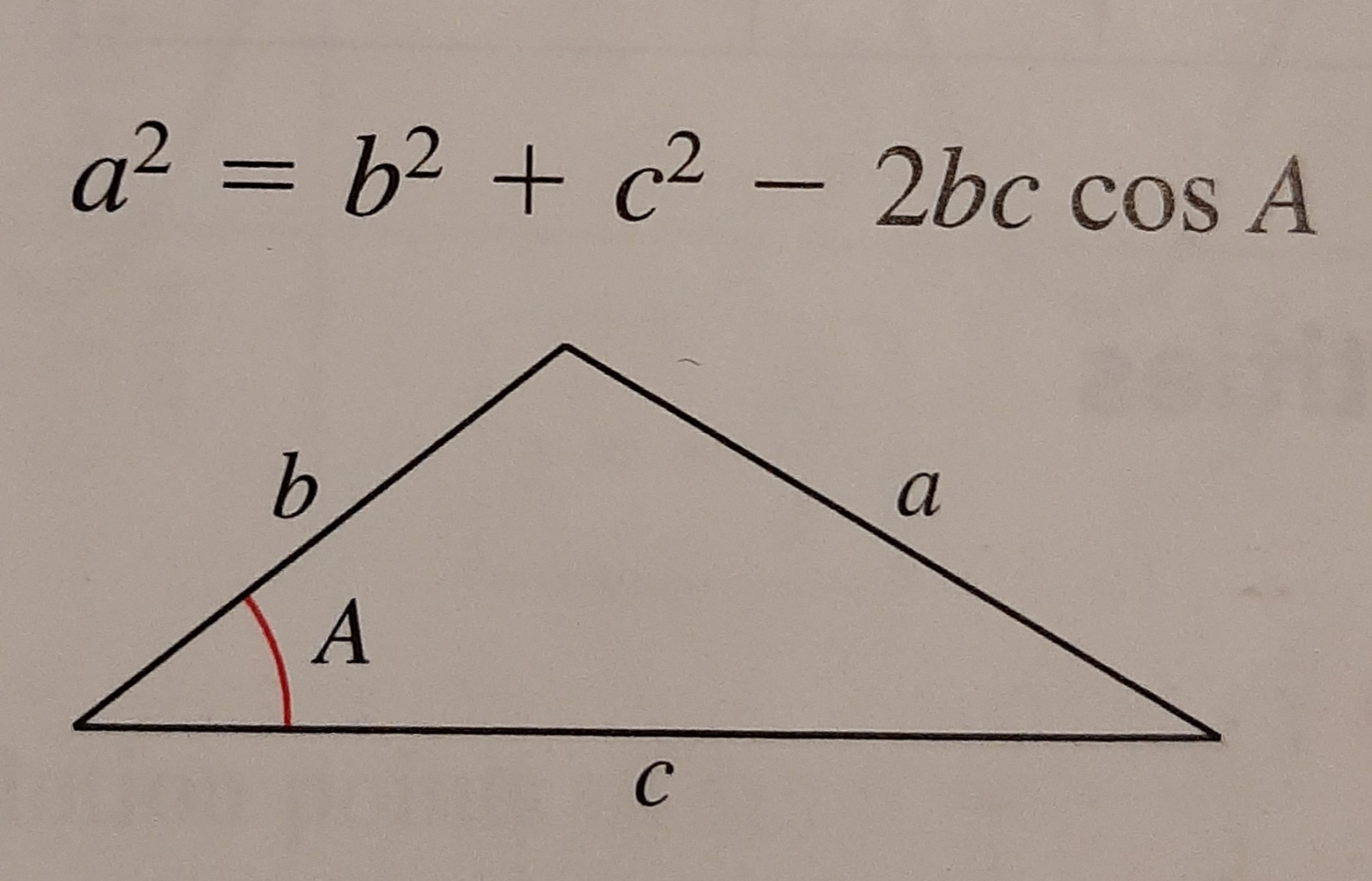
Law of Cosines
- $\sin^{2}{\theta} = \frac{1 - \cos{2\theta}}{2}$
- $\cos^{2}{\theta} = \frac{1 + \cos{2\theta}}{2}$
- $\tan^{2}{\theta} = \frac{1 - \cos{2\theta}}{1 + \cos{2\theta}}$
- $\sin{2\theta} = 2 \sin{\theta} \cos{\theta}$
- $\cos{2\theta} = $
- $2 \cos^{2}{\theta} - 1$
- $1 - 2 \sin^{2}{\theta}$
- $\cos^{2}{\theta} - \sin^{2}{\theta}$
- $\tan{2 \theta} = \frac{2 \tan{\theta}}{1 - \tan^{2}{\theta}}$
Common Trig Values
| |
|
|
|
|
|
|
|
| Degrees |
$0^\circ$ |
$30^\circ$ |
$45^\circ$ |
$60^\circ$ |
$90^\circ$ |
$180^\circ$ |
$270^\circ$ |
| Radians |
$0$ |
$\pi/6$ |
$\pi/4$ |
$\pi/3$ |
$\pi/2$ |
$\pi$ |
$3\pi/2$ |
| $\sin{\theta}$ |
$0$ |
$1/2$ |
$\sqrt{2}/2$ |
$\sqrt{3}/2$ |
$1$ |
$0$ |
$-1$ |
| $\cos{\theta}$ |
$1$ |
$\sqrt{3}/2$ |
$\sqrt{2}/2$ |
$1/2$ |
$0$ |
$-1$ |
$0$ |
| $\tan{\theta}$ |
$0$ |
$\sqrt{3}/3$ |
$1$ |
$\sqrt{3}$ |
Undefined |
$0$ |
Undefined |
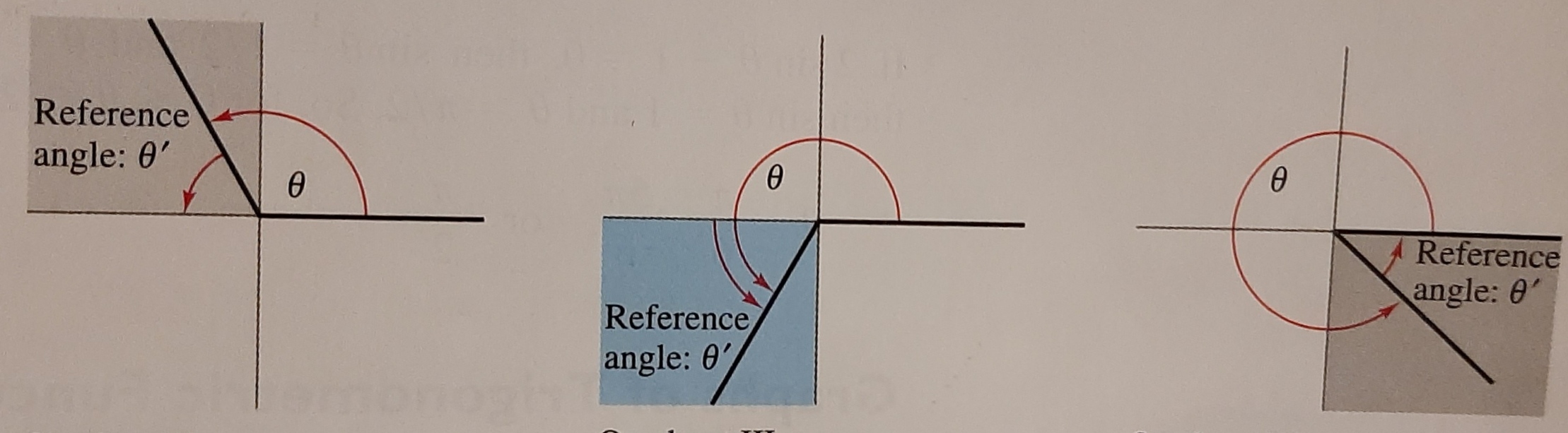
Reference angles
Reference angles can be used to know the values fir angles in other quadrants besides the 1st quadrant.

The reference angle is always based off the x-axis.
Solving Trig Equations
- Find the angle in the 1st quadrant(assume the value is positive).
- Find all the quadrants that match the value’s sign.
- Calculate all reference angles.
- Since trig functions osculate, you have to add $2\pi n$ to your angles.
Example: $\sin{\theta} = - \sqrt{3} / 2$
- $\sin{\theta} = \sqrt{3} / 2 = \sin{(\pi / 3)}$
- Quadrants 3 and 4 are where $\sin$ is negative.
- Use reference angle to convert:
- Quadrant 3: $\pi + \frac{\pi}{3} = \frac{4 \pi}{3}$
- Quadrant 4: $2 \pi - \frac{\pi}{3} = \frac{5 \pi}{2}$
- $\frac{4 \pi}{3} + 2 \pi n$ and $\frac{5 \pi}{3} + 2 \pi n$



